本文共 2890 字,大约阅读时间需要 9 分钟。
这里我想给大家介绍另外一种推荐系统,这种算法叫做潜在因子(Latent Factor)算法。这种算法是在NetFlix(没错,就是用大数据捧火《纸牌屋》的那家公司)的推荐算法竞赛中获奖的算法,最早被应用于电影推荐中。这种算法在实际应用中比现在排名第一的 所介绍的算法误差(RMSE)会小不少,效率更高。我下面仅利用基础的矩阵知识来介绍下这种算法。
这种算法的思想是这样:每个用户(user)都有自己的偏好,比如A喜欢带有小清新的、吉他伴奏的、王菲等元素(latent factor),如果一首歌(item)带有这些元素,那么就将这首歌推荐给该用户,也就是用元素去连接用户和音乐。每个人对不同的元素偏好不同,而每首歌包含的元素也不一样。我们希望能找到这样两个矩阵:
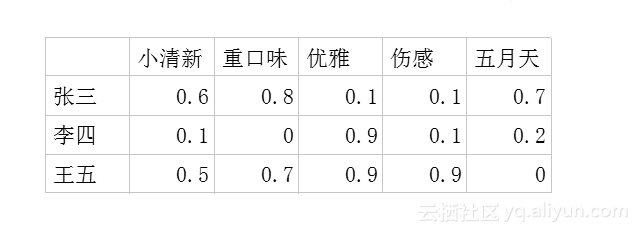
一.用户-潜在因子矩阵Q,
表示不同的用户对于不用元素的偏好程度,1代表很喜欢,0代表不喜欢。比如下面这样:
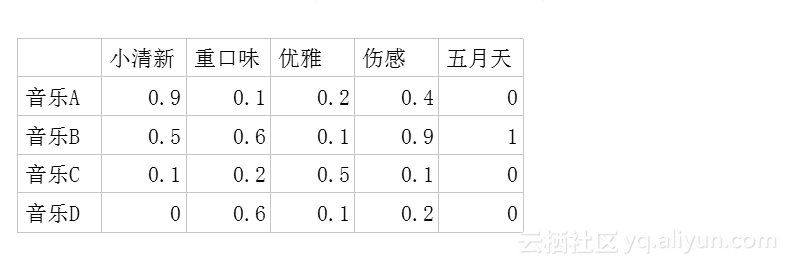
二.潜在因子-音乐矩阵P
表示每种音乐含有各种元素的成分,比如下表中,音乐A是一个偏小清新的音乐,含有小清新这个Latent Factor的成分是0.9,重口味的成分是0.1,优雅的成分是0.2……
利用这两个矩阵,我们能得出张三对音乐A的喜欢程度是:张三对小清新的偏好*音乐A含有小清新的成分+对重口味的偏好*音乐A含有重口味的成分+对优雅的偏好*音乐A含有优雅的成分+……
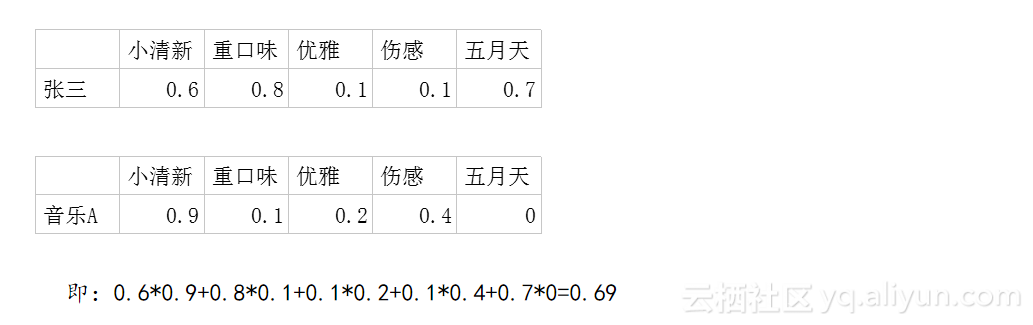
即:0.6*0.9+0.8*0.1+0.1*0.2+0.1*0.4+0.7*0=0.69
每个用户对每首歌都这样计算可以得到不同用户对不同歌曲的评分矩阵。(注,这里的破浪线表示的是估计的评分,接下来我们还会用到不带波浪线的R表示实际的评分):
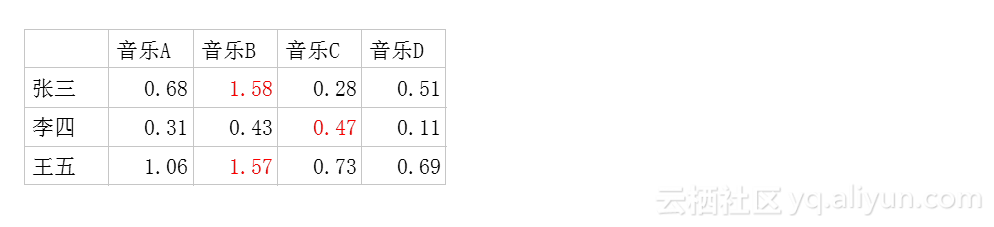
因此我们队张三推荐四首歌中得分最高的B,对李四推荐得分最高的C,王五推荐B。
如果用矩阵表示即为:
下面问题来了,这个潜在因子(latent factor)是怎么得到的呢?
由于面对海量的让用户自己给音乐分类并告诉我们自己的偏好系数显然是不现实的,事实上我们能获得的数据只有用户行为数据。我们沿用 的量化标准:单曲循环=5, 分享=4, 收藏=3, 主动播放=2 , 听完=1, 跳过=-2 , 拉黑=-5,在分析时能获得的实际评分矩阵R,也就是输入矩阵大概是这个样子:
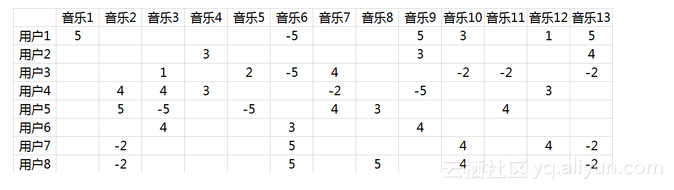
事实上这是个非常非常稀疏的矩阵,因为大部分用户只听过全部音乐中很少一部分。如何利用这个矩阵去找潜在因子呢?这里主要应用到的是矩阵的UV分解。也就是将上面的评分矩阵分解为两个低维度的矩阵,用Q和P两个矩阵的乘积去估计实际的评分矩阵,而且我们希望估计的评分矩阵
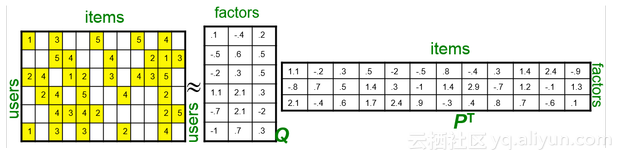
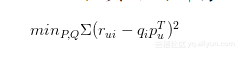
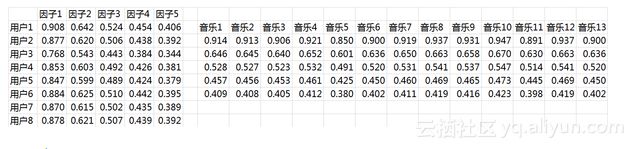
这两个矩阵相乘就可以得到估计的得分矩阵:
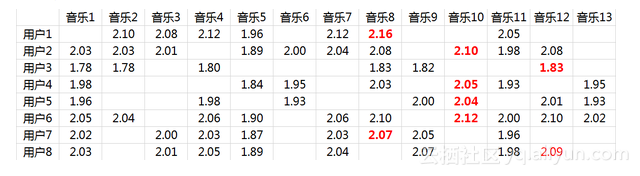 将用户已经听过的音乐剔除后,选择分数最高音乐的推荐给用户即可(红体字)。
将用户已经听过的音乐剔除后,选择分数最高音乐的推荐给用户即可(红体字)。 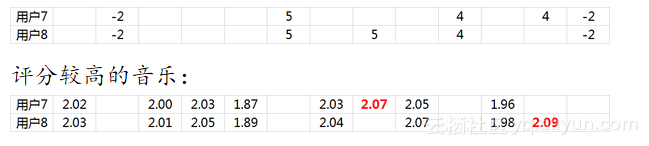
###########################################################################################
具体公式:
下面我们就来看看LFM是如何解决上面的问题的?对于一个给定的用户行为数据集(数据集包含的是所有的user, 所有的item,以及每个user有过行为的item列表),使用LFM对其建模后,我们可以得到如下图所示的模型:(假设数据集中有3个user, 4个item, LFM建模的分类数为4)
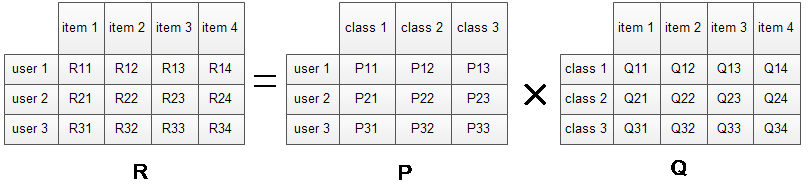
R矩阵是user-item矩阵,矩阵值Rij表示的是user i 对item j的兴趣度,这正是我们要求的值。对于一个user来说,当计算出他对所有item的兴趣度后,就可以进行排序并作出推荐。LFM算法从数据集中抽取出若干主题,作为user和item之间连接的桥梁,将R矩阵表示为P矩阵和Q矩阵相乘。其中P矩阵是user-class矩阵,矩阵值Pij表示的是user i对class j的兴趣度;Q矩阵式class-item矩阵,矩阵值Qij表示的是item j在class i中的权重,权重越高越能作为该类的代表。所以LFM根据如下公式来计算用户U对物品I的兴趣度
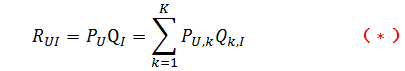
我们发现使用LFM后,
- 我们不需要关心分类的角度,结果都是基于用户行为统计自动聚类的,全凭数据自己说了算。
- 不需要关心分类粒度的问题,通过设置LFM的最终分类数就可控制粒度,分类数越大,粒度约细。
- 对于一个item,并不是明确的划分到某一类,而是计算其属于每一类的概率,是一种标准的软分类。
- 对于一个user,我们可以得到他对于每一类的兴趣度,而不是只关心可见列表中的那几个类。
- 对于每一个class,我们可以得到类中每个item的权重,越能代表这个类的item,权重越高。
那么,接下去的问题就是如何计算矩阵P和矩阵Q中参数值。一般做法就是最优化损失函数来求参数。在定义损失函数之前,我们需要准备一下数据集并对兴趣度的取值做一说明。
数据集应该包含所有的user和他们有过行为的(也就是喜欢)的item。所有的这些item构成了一个item全集。对于每个user来说,我们把他有过行为的item称为正样本,规定兴趣度RUI=1,此外我们还需要从item全集中随机抽样,选取与正样本数量相当的样本作为负样本,规定兴趣度为RUI=0。因此,兴趣的取值范围为[0,1]。 采样之后原有的数据集得到扩充,得到一个新的user-item集K={(U,I)},其中如果(U,I)是正样本,则RUI=1,否则RUI=0。损失函数如下所示:
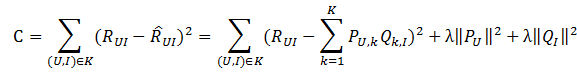
上式中的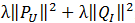
- 通过求参数PUK和QKI的偏导确定最快的下降方向;
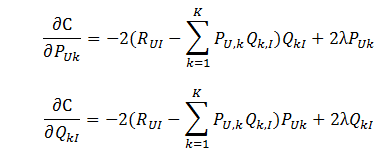
- 迭代计算不断优化参数(迭代次数事先人为设置),直到参数收敛。
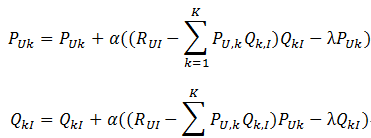
其中,α是学习速率,α越大,迭代下降的越快。α和λ一样,也需要根据实际的应用场景反复实验得到。本书中,作者在数据集上进行实验,他取分类数F=100,α=0.02,λ=0.01。 综上所述,执行LFM需要:
- 根据数据集初始化P和Q矩阵(这是我暂时没有弄懂的地方,这个初始化过程到底是怎么样进行的,还恳请各位童鞋予以赐教。)
- 确定4个参数:分类数F,迭代次数N,学习速率α,正则化参数λ。
1.相关文档
http://blog.csdn.net/sinat_33741547/article/details/52976391
http://www.cnblogs.com/tbiiann/p/6535189.html
http://www.cnblogs.com/hxsyl/p/4885372.html